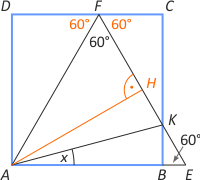
Zad. 1. Na odcinku AB obrano punkt P i zbudowano okręgi o średnicach AP i PB. Sieczna AK pierwszego okręgu jest styczna w punkcie C do drugiego okręgu. Prosta CP przecina pierwszy okrąg w punkcie L. Wiedząc, że |AK|=5 i |KC|=25, oblicz pole trójkąta LBP.
Zad. 2. W kwadrat ABCD wpisano trójkąt równoboczny ABE. Prosta CE przecina bok AD w punkcie F. Wiedząc, że |FE|=6, oblicz pole trójkąta FCD.
Zad. 3. Niech M będzie środkiem boku BC kwadratu ABCD, a AH - wysokością trójkąta AMD. Wiedząc, że |HB|=8, oblicz pole kwadratu.
Zad. 4. (wolna amerykanka) Dany jest kwadrat ABCD. Na boku CD obrano punkt F, a na prostej AB - punkt E takie, że trójkąt AEF jest równoboczny. Proste BC i EF przecinają się w punkcie K. Oblicz miarę kąta KAE.
W tym miesiącu za zadania 1-3 punkty otrzymali:
- 30 - Elżbieta Grzechnik (emerytowana nauczycielka z Radomia), Szymon Kaźmierowski (nauczyciel z Elbląga), Mikołaj Popek (student UAM), Tadeusz Porzucek (emerytowany nauczyciel z Gostynia) i Marzena Wąsiewicz (nauczycielka z Kajetan),
- 20 - Iwona Gruszecka (nauczycielka w CLV LO Warszawa) oraz Janusz Wieczorek (emerytowany nauczyciel z Sandomierza).
Za zadanie 4 po 10 pkt. otrzymali: Iwona Gruszecka, Elżbieta Grzechnik, Szymon Kaźmierowski, Zygmunt Krawczyk (emerytowany nauczyciel ze Szprotawy), Szymon Meyer (analityk danych z Dziewkowic), Mikołaj Popek, Tadeusz Porzucek, Marzena Wąsiewicz oraz Janusz Wieczorek.
Gratulujemy!
Zad. 1. Zauważmy, że czworokąt ALBC jest trapezem, bo kąty ALC i LCB są proste (jako oparte na średnicach AP i PB). Zauważmy dalej równość pól: PLPB = PLBC – PPBC = PABC – PPBC = PAPC. Wystarczy zatem obliczyć PAPC. Z twierdzenia Talesa mamy |AK|/|KC| = |AD|/|PO| = 1/5. Oznaczmy |AP|=d. Wówczas |PO|=5d i |PB|=10d. Z twierdzenia potęgowego o stycznej i siecznej okręgu mamy |AC|2=|AP|·|AB|, skąd otrzymujemy równanie 900=11d2 i dalej d2=900/√11. Z twierdzenia Pitagorasa w trójkącie APK mamy |PK|=25/√11. Ostatecznie PLPB=PAPB= 375/√11.
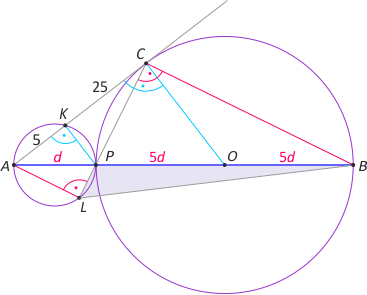
Zad. 2. Z założenia trójkąt EBC jest równoramienny przy czym |∡EBC|=30° oraz |∡ECB|=75°. Stąd |∡FCD|=15°. Niech punkt G będzie symetrycznym do F względem wierzchołka D. Wówczas trójkąty FCD i DCG są przystające, a stąd |∡FCG|=30° oraz |FC|=|CG|. Łatwo zauważyć, że |FC|=2|FE|=12. Niech GH będzie wysokością w trójkącie FCG. Wówczas z trójkąta "ekierkowego" HCG mamy |GH|=|GC|/2=6. Ostatecznie PFCD = PFCG/2 = 18.
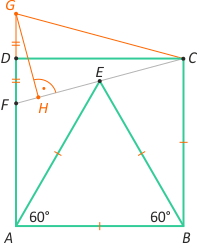
Zad. 3. Przedłużmy odcinek DM do przecięcia się z prostą AB w punkcie E. Trójkąty BEF i MCD są przystające (cecha kbk). Oznaczmy |AB|=x. Wówczas |BE|=x i z faktu, że środkowa przeciwprostokątnej jest od niej dwa razy krótsza, w trójkącie AEH mamy x=8. Ostatecznie PABCD=64.
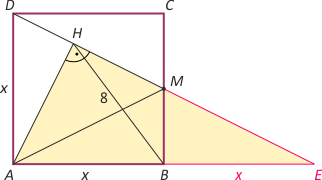
Zad. 4. (wolna amerykanka) Niech AH będzie wysokością w trójkącie AEF. łatwo zauważyć, że trójkąty AFD i AHF są przystające, przy czym |AH|=|AD| i |∡DAF|=|∡FAH|=30°, a stąd |∡HAB|=30°. Zauważmy teraz przystawanie trójkątów prostokątnych ABK i AKH (mają wspólną przeciwprostokątną AK i przystające przyprostokątne AH i AB). Oznacza to, że |∡BAK|=15°.
To zabawny samouczek, który zaczynając się niewinnie intrygującą historyjką, krok po kroku, poczynając od najłatwiejszych łamigłówek, prowadzi nas w szpony, nie bójmy się użyć tego słowa, uzależnienia.
